Pythagoras 
und die 
Mathematik

Allgemein

Pythagoras von Samos
Ulrich Holzmann, Roman Mally
,,Im rechtwinkligen Dreieck ist die Summe der Kathetenquadrate gleich dem Hypotenusenquadrat." Diese Worte, auch als Satz des Pythagoras bekannt, werden dem Lebenswerk des Pythagoras von Samos oftmals gleichgesetzt (Es gibt über 100 Beweise für den Satz! Einige davon sind auf werden auf dieser Seite vorgeführt). Wie aber folgende Zitate erkennen lassen, war dieser Mensch noch viel mehr.

,,Er ist einer der bedeutendsten Menschen" - Bertrand Russel
,,Er ist der Anführer der Schwindler" - Heraklid
,,Der wise Pictagoras, der ein astronomierre was" - Wolfram von Eschenbach

Ludwig Börne über ihn: ,,Als er den Satz gefunden hatte, soll er den Göttern hundert Ochsen geopfert haben. Seitdem zittern alle Ochsen, sooft eine neue Wahrheit entdeckt wird."
http://www.didmath.ewf.uni-erlangen.de/Vorlesungen/Pythago/Pythagoras.html

http://www.stud.uni-bayreuth.de/~a3957/pythagoras/1.1/p1.html

Der Satz des Pythagoras
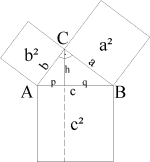
Der Lehrsatz des Pythagoras a² + b² = c² wird bewiesen. Die Schalter NEXT, BACK und RESET erlauben einen Gang durch den Beweis.
http://didaktik.physik.uni-wuerzburg.de/~pkrahmer/java/pythago/pythago.html

Der Satz des Pythagoras
Schon vor Pythagoras (ca. 580-500 v. Chr.) war der Satz des Pythagoras bekannt. In den altbabylonischen, ägyptischen, indischen und chinesischen Texten mathematischen Inhalts werden in der Regel konkrete Aufgaben gestellt, deren Lösungen in Form von rezeptartigen Rechenvorschriften mitgeliefert werden. Dabei wird die Lösung in vielen Fällen zwar mit konkreten Zahlen durchgeführt, ist aber so konzipiert, daß sie sich unmittelbar verallgemeinern läßt. Ebenso werden Begründungen - falls sie überhaupt gegeben werden - nur für den konkreten Fall formuliert, oder man beschränkt sich auf eine beigefügte Figur und den berühmten Hinweis: "Siehe!". In Griechenland war wohl Pythagoras von Samos einer der ersten, der ein Berechnungsverfahren für spezielle pythagoreische Zahlentripel angab, ob er den nach ihm benannten Lehrsatz für beliebige rechtwinklige Dreiecke gekannt hat ist allerdings nicht bekannt, da keine schriftlichen Aufzeichnungen darüber existieren. Der älteste bekannte schriftliche Beweis des Satzes aus Griechenland stammt von Euklid (um 365 v. Chr. geb.). Griechische Mathematiker vor Euklid dürften allerdings bereits einen Ähnlichkeitsbeweis für den Pythagorassatz gekannt haben. Für den Lehrsatz des Pythagoras kennt man heute über 400 Beweise. Einige davon werden auf diesen Seiten vorgestellt (teilweise mit JAVA-Scripts).
http://did.mat.uni-bayreuth.de/seminar/hypermed1/klarner/seite.htm

Beweistechniken an der Satzgruppe des Pythagoras
Christian Nöth
Die Sätze der Satzgruppe des Pythagoras helfen uns zahlreiche mathematische Fragestellungen bei Konstruktionen, Beweisen, Herleitungen von Formeln etc. zu beantworten. Das Anwenden dieser Sätze ermöglicht es uns z. B. Längenberechnungen bei Strecken in der Ebene und in der Raumgeometrie durchzuführen. Weitere Einsatzgebiete sind z. B. die analytische Geometrie und Trigonometrie. Die Satzgruppe des Pythagoras beinhaltet folgende Sätze:

      Satz des Pythagoras                                 Höhensatz                                 Kathetensatz

Auf den folgenden Seiten finden Sie neben den Formulierungen der Sätze, verschiedene Beweise und Beweistechniken, Übungen, Zusammenhänge unter den Sätzen, deren Umkehrungen und Prinzipien (z. B. Spezialisierung).
http://www.mathematik.uni-wuerzburg.de/Didaktik/pythagoras/index.html

The Pythagorean Theorem
Timothy Reluga
Evidence of the theorem can be traced far back into Egyptian history with the help of the Rhind Papyrus(1788-1580 BC). The Rhind Papyrus itself claims to be a copy of an earlier work, possibly dating as far back as 2000 BC. The use of the 3-4-5 triangles(9+16=25) to construct perfect right angles, indeed seems to have been a very common practice, long ago. Unfortunately, little information predates the Greeks, so this will probably remain another mystery of the Egyptians. Traditionally, however, the theorem has been credited [in western culture] to Pythagoras of Samos. The legend has it that he was so excited by its proof that he sacrificed a bull for the occasion, even though Pythagoreans were against animal sacrifice. Unfortunately, there are only legends. The Pythagorean School, which gets its name from its founder, was a secret cult. They regarded their knowledge as something to be kept from all outsiders. Thus, they did not write things down until the cult began to lose prominence several generations later, leaving posterity with a void where the life of Pythagoras should have been. Consequently, classicists do not know if Pythagoras was actually responsible for the first proof.
http://www.perseus.tufts.edu/GreekScience/Students/Tim/Pythag'sTheorem.html

Pythagoras - Tripel
Heinz Becker - heinzbecker@foni.net
Downloadbares Programm für Pythagoras-Zahlentripel. Auch als direkt lauffähiges JAVA-Scsript.
http://home.foni.net/~heinzbecker/hbnms.htm