Mathematik

Allgemein

PROJECTIVE GEOMETRY
Nick Thomas - nct@cix.compulink.co.uk
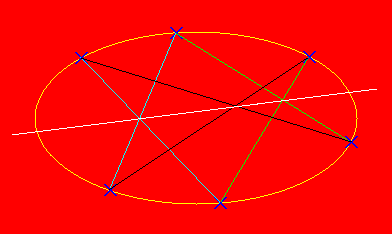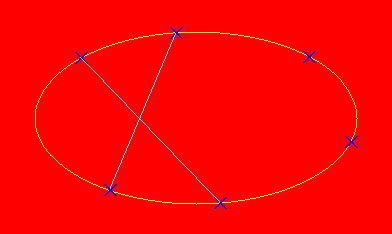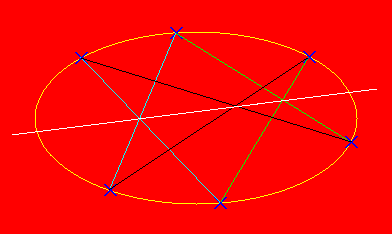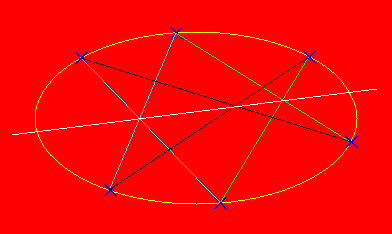Projective geometry is a beautiful subject which has some remarkable applications beyond those in standard textbooks.  These were pointed to by Rudolf Steiner who sought an exact way of working scientifically with aspects of reality which cannot be described in terms of ordinary physical measurements.  His colleague George Adams worked out much of this and pointed the way to some remarkable research done by Lawrence Edwards in recent years.  Steiner's spiritual research showed that there is another kind of space in which more subtle aspects of reality such as life processes take place.   Adams took his descriptions of how this space is experienced and found a way of specifying it geometrically, which is dealt with in the Counter Space Page.
A brief introduction to the basics of the subject is given in the Basics Page.
The work of Lawrence Edwards is introduced in the Path Curves Page, and some explorations of his work on further aspects is described in the Pivot Transforms Page. This is mostly pictorial, with reference to documentation.
http://www.anth.org.uk/NCT/

Für welche Zahlenpaare ist das Potenzieren kommutativ ?
Dieter Kötter - e-mail: d.koetter@t-online.de
Während für die erste und zweite Rechenstufe a+b = b+a bzw. a·b = b·a gilt, ist bei der dritten Rechenstufe, dem Potenzieren im allgemeinen a^b ¹ b^a . Jeder kennt jedoch das Beispiel 2⁴ = 4² . Man kann sich die Frage vorlegen, welche weiteren Zahlenpaare (x/y) es gibt, für die x^y = y^x gilt . Wir werden im Folgenden solche Zahlenpaare potenzkommutativ nennen.
http://home.t-online.de/home/d.koetter/potenz.html